Muzyka, podobnie jak matematyka, stanowi uniwersalny język, który pozwala nam się zrozumieć bez słów. Choć pozornie są to zupełnie odległe dziedziny w naszym życiu, okazują się mieć ze sobą więcej wspólnego niż mogłoby się wydawać na pierwszy rzut oka.
Pozostając w weekendowym klimacie, chcielibyśmy w ramach ciekawostki przedstawić Wam, drodzy Czytelnicy, kolejne spostrzeżenia jakie udało nam się poczynić w zupełnym oderwaniu od wykresów i analiz, a oddając się jednej z najprzyjemniejszych czynności – obcowaniu z muzyką.
Czy Leonardo Fibonacci był fanem muzyki fortepianowej? – tego nie wiemy, możemy jednak z całą pewnością stwierdzić, że jego praca wywarła znaczący wpływ na niejednego kompozytora. Poczynając od wyglądu fortepianowej klawiatury, kończąc na strukturze muzycznych kompozycji, liczby Fibonacciego przemycają w świat muzyki swoistą harmonię i sekwencyjny porządek. Nie trzeba być pianistą by go odkryć, ale z całą pewnością pomocna będzie natura poszukiwacza oraz dociekliwość charakteryzująca każdego dobrego tradera. Gdzie zatem szukać wspomnianych zależności?
Dźwięki na liczbach fibo…
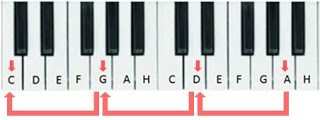
 Każdy kto przyglądał się choć przez moment fortepianowej klawiaturze, miał okazję zorientować się w pewnych prawidłowościach zauważalnych w jej budowie. Spoglądając na powyższe zdjęcie nietrudno zauważyć, że pianino śpiewa liczbami fibo. Osiem białych klawiszy tworzy podstawowy interwał muzyczny – oktawę (C-D-E-F-G-A-H-C). Pomiędzy nimi odnajdujemy pięć czarnych dźwięków, które wraz z białymi dają nam trzynaście tonów w oktawie. Czarne klawisze podzielone zostały na grupy po dwa i po trzy w każdej oktawie. Dominantą jest stopień piąty (na powyższym zdjęciu – G), będący jednocześnie ósmym w trzynastostopniowej skali. Stanowi on jeden z trzech głównych stopni gamy służących do budowy trójdźwięków (najprostszych akordów składających się z trzech dźwięków), tworzących tak zwaną triadę harmoniczną (trzy podstawowe trójdźwięki), która budowana jest na określonych stopniach pięciolinii (C-E-G, F-A-C, G-H-D). Są to tzw. akordy główne.
Każdy kto przyglądał się choć przez moment fortepianowej klawiaturze, miał okazję zorientować się w pewnych prawidłowościach zauważalnych w jej budowie. Spoglądając na powyższe zdjęcie nietrudno zauważyć, że pianino śpiewa liczbami fibo. Osiem białych klawiszy tworzy podstawowy interwał muzyczny – oktawę (C-D-E-F-G-A-H-C). Pomiędzy nimi odnajdujemy pięć czarnych dźwięków, które wraz z białymi dają nam trzynaście tonów w oktawie. Czarne klawisze podzielone zostały na grupy po dwa i po trzy w każdej oktawie. Dominantą jest stopień piąty (na powyższym zdjęciu – G), będący jednocześnie ósmym w trzynastostopniowej skali. Stanowi on jeden z trzech głównych stopni gamy służących do budowy trójdźwięków (najprostszych akordów składających się z trzech dźwięków), tworzących tak zwaną triadę harmoniczną (trzy podstawowe trójdźwięki), która budowana jest na określonych stopniach pięciolinii (C-E-G, F-A-C, G-H-D). Są to tzw. akordy główne.
„We follow nature in composition…”
Wielu kompozytorów inspirując się sekwencją Leonarda oparło strukturę swoich utworów o konkretne wartości ciągu. Jednym z nich był pochodzący z Węgier Bela Bartók. Zafascynowany przyrodą gromadził imponujące kolekcje roślin, czy minerałów upatrując natury żywych organizmów w muzyce, która podobnie jak one, ewoluuje i rozwija się spontanicznie. Wydaje się, że naturalną dla kompozytora rzeczą była adaptacja w muzyce praw matematycznych, które jako wnikliwy obserwator dostrzegał wokół siebie. Doskonałym na to przykładem jest znajdujący się w jego dorobku utwór „Muzyka na instrumenty strunowe, perkusję i czelestę”. Kompozycja powstała w 1936 roku, na zamówienie dyrygenta Paula Sachera z okazji dziesiątej rocznicy Bazylejskiej Orkiestry Kameralnej.
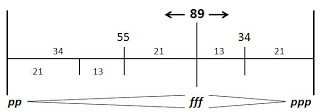
Ernö Lendvai – schemat budowy utworu B. Bartóka z podziałem na poszczególne części kompozycji.
W jaki sposób Bartók stworzył swój utwór? Jego budowa oparta jest o 89 taktów, natomiast kulminacyjny moment kompozycji przypada na takt 55. Ekspozycja, czyli część rozpoczynająca, kończy się po 21 taktach. Kolejne instrumenty wchodzą w następującym porządku: altówka 1,2 – takt pierwszy, altówka 3,4 – takt piąty, wiolonczela 1,2 – takt ósmy, skrzypce 2 – takt trzynasty. Przyglądając się zapisom nutowym zauważyć można pojawiające się pojęcia „senza sord.” oraz „con sord.”. W artykulacji muzycznej „senza sordino” oraz „con sordino” oznaczają określony sposób wydobycia dźwięku przy wykorzystaniu charakterystycznego dla poszczególnych instrumentów tłumika. W utworze Bartóka tłumik dla skrzypiec zanika od taktu 34, by pojawiać się w zapisie ponownie od taktu 69.
Fragment zapisu nutowego utworu B. Bartóka – takt 34 z oznaczeniem „senza sord” dla skrzypiec.
Ponadto w utworze kolejne powtórzenia głównego tematu rozpoczynają się w odległości kwinty od siebie (jest to interwał muzyczny zawarty pomiędzy kolejnymi pięcioma stopniami skali), tworząc powtarzający się wzrastająco lub malejąco schemat dźwięków: A – E – B – F♯-… itd. oraz A – D – G – C – … itd.
Bartók nie był jedynym kompozytorem wykorzystującym zależności ciągu Fibonacciego w swojej muzyce. Również ZoltánKodály, czy znany Claoude Debussy, którzy mieli znaczny wpływ na twórczość Beli, wykorzystywali w swoich dziełach złotą proporcję. Nie sposób również nie wspomnieć o polskim kompozytorze, który w swojej twórczości posługuje się liczbami sekwencji oraz złotym podziałem. Krzysztof Meyer znany jest z takich utworów jak: „Trio klarnetowe”, „Msza”, czy „VII kwartet smyczkowy”. Już w pierwszej wspomnianej kompozycji zauważyć można matematyczną regularność wynikającą z ciągu, gdzie wszystkie instrumenty grają kolejno 21, 34, 55, 89, 144 ćwierćnut, natomiast kolejne odcinki dzieła przypisane pod fortepian liczą sobie odpowiednio 89, 55, 34, 21 oraz 12 ćwierćnut, na bazie których zbudowana jest kompozycja.
Tych kilka przykładów zilustrowanych tutaj dowodzi jak unikalną i jednocześnie wielokierunkową nauką jest matematyka. Przytoczeni kompozytorzy to jedynie przedstawiciele znacznie szerszych grup artystów zainteresowanych poszukiwaniem harmonii oraz tworzeniem w oparciu o jednolite i uniwersalne prawa występujące w naturze. Wciąż pozostaje pytanie, jak wiele z powszechnie znanych przykładów występowania magicznego ciągu Fibonacciego rodzi się w efekcie świadomego dążenia do osiągnięcia harmonicznego ładu, ile natomiast wynika z samoistnych praw natury, które wciąż obserwujemy i które nieustannie nas zaskakują?