Zastanawiałeś się z pewnością jak to jest, że patrząc na jeden wykres konkretnej pary walutowej widzisz kilka różnych układów, a tym samym nie masz pewności co do wykonanej analizy ani (co gorsza) do kierunku przyszłego wejścia w pozycję.
Podczas najbliższego video-czatu z cyklu Matematyka na FX:
1. Po raz pierwszy przedstawimy oraz szczegółowo omówimy Miner’owską koncepcję DTFM,
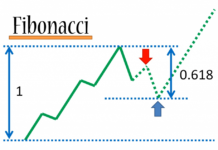
2. Od strony matematycznej wyznaczymy na podstawie konkretnych działań różnicę jaką jesteśmy w stanie zaakceptować- szacując w ten sposób „odchylenie Fibonacciego”,
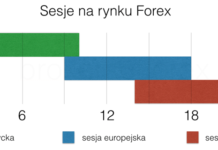
3. Zobacz jak wygląda prosta strategia określania „swobodnego obszaru” rynkowego określonego za pomocą podwójnych przedziałów czasowych.
Dodatkowo na przykładzie konkretnych transakcji odpowiemy na najczęstsze pytania dotyczące:
• Precyzji zajęcia pozycji: „co zrobić ze stopem jeśli pozycja mi ucieka”?
• Interwału czasowego: „czy istnieje uniwersalny TimeFrame i czy to ma znaczenie dla wielkości pozycji oraz wielkości mojego Stop Lossa”?
• Procentowego opóźnienia sygnału względem pierwotnej koncepcji: kiedy nie jest za „późno” aby zająć pozycję?
